Understanding 365/360 Loan Calculation Methods
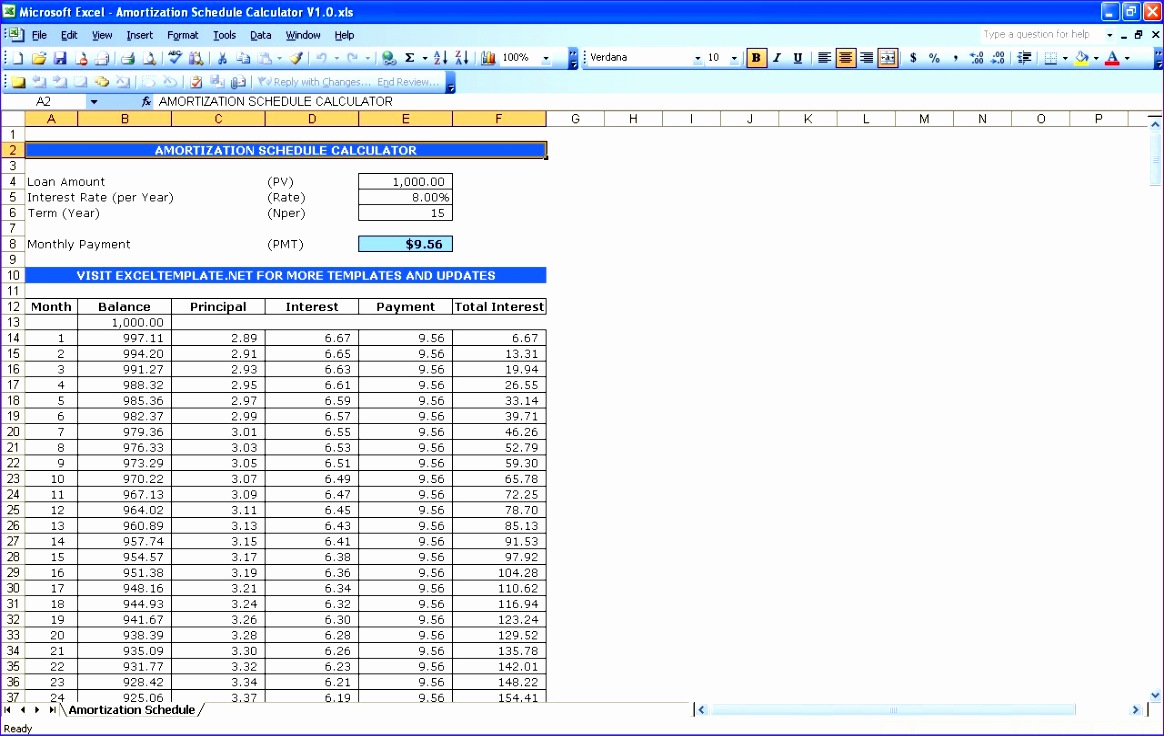
Choosing the right loan calculation method significantly impacts the total interest you pay. While seemingly minor, the difference between a 365-day and a 360-day year can lead to surprisingly large discrepancies over the life of a loan. Understanding these nuances is crucial for both borrowers and lenders to make informed financial decisions.
365-Day vs. 360-Day Loan Calculations
The core difference lies in the number of days used to calculate the daily interest rate. The 365-day method uses the actual number of days in a year, accounting for leap years. The 360-day method, often called the “banker’s year,” simplifies calculations by consistently using 360 days. This simplification might seem trivial, but its cumulative effect on interest accrual can be substantial, especially for longer-term loans.
Impact on Interest Accrual
The 360-day method generally results in slightly higher daily interest rates compared to the 365-day method. This is because the same annual interest is spread over fewer days. Consequently, borrowers using the 360-day method will pay slightly more interest over the loan’s lifetime. The difference might seem negligible on smaller loans or short loan terms, but it becomes more pronounced as the loan amount and term increase.
Comparative Analysis: Total Interest Paid
Let’s illustrate with an example. Consider a $10,000 loan with a 5% annual interest rate over a 5-year term. Using a 365-day calculation, the total interest paid would be approximately $2,580. Using a 360-day calculation, the total interest paid would be slightly higher, approximately $2,604. The difference, although seemingly small, is a tangible $24 over five years. This discrepancy highlights the importance of understanding the subtle differences between these methods.
Step-by-Step Calculation Examples
To illustrate the calculation process, let’s use the same loan parameters ($10,000 loan, 5% annual interest, 5-year term).
365-Day Method:
1. Calculate the daily interest rate: 5% annual interest / 365 days = 0.0137% daily interest rate.
2. Calculate the daily interest: $10,000 * 0.000137 = $1.37 daily interest (approximately).
3. Calculate the total interest over 5 years (1825 days): $1.37 * 1825 = $2502.75 (approximately). Note: This is a simplified calculation, not accounting for compounding. A true calculation would require amortization calculations.
360-Day Method:
1. Calculate the daily interest rate: 5% annual interest / 360 days = 0.0139% daily interest rate.
2. Calculate the daily interest: $10,000 * 0.000139 = $1.39 daily interest (approximately).
3. Calculate the total interest over 5 years (1800 days assuming 12 months of 30 days each): $1.39 * 1800 = $2502 (approximately). Again, this is a simplified calculation and doesn’t account for compounding.
Comparison of 365 and 360-Day Loan Calculations
| Method | Calculation Basis | Interest Impact | Example ($10,000 loan, 5%, 5 years) |
|---|---|---|---|
| 365-Day | Actual number of days in a year | Lower total interest paid | Approximately $2502.75 (simplified) |
| 360-Day | 360 days per year | Higher total interest paid | Approximately $2502 (simplified) |
Excel Implementation of 365/360 Loan Calculators
Building a loan calculator in Excel allows for dynamic and flexible loan analysis. Understanding the nuances of the 365-day and 360-day methods is crucial for accurate calculations, particularly in financial modeling and forecasting. This section details the Excel formulas and steps for implementing both methods.
Loan Payment Calculation using the 365-Day Method
The 365-day method uses a year of 365 days for interest calculations. This formula provides greater accuracy, especially for long-term loans. The core of the calculation relies on the PMT function in Excel.
=PMT(rate/365, nper*365, pv, [fv], [type])
Where:
* rate: The annual interest rate (expressed as a decimal, e.g., 0.05 for 5%).
* nper: The loan term in years.
* pv: The present value (loan amount), entered as a negative value.
* fv: The future value (optional, defaults to 0).
* type: Specifies when payments are due (0 for end of period, 1 for beginning; defaults to 0).
This formula divides the annual interest rate by 365 to get the daily rate, and multiplies the loan term (in years) by 365 to get the total number of payment periods. For example, a $10,000 loan at 5% annual interest for 5 years would be: =PMT(0.05/365, 5*365, -10000). The result will be the monthly payment amount. Note that the result will be a negative number, indicating a cash outflow.
Loan Payment Calculation using the 360-Day Method
The 360-day method simplifies calculations by assuming a year consists of 360 days. While less precise than the 365-day method, it’s often used for its simplicity and is still widely accepted in many financial contexts. The Excel formula remains similar:
=PMT(rate/360, nper*360, pv, [fv], [type])
The only difference is that the annual interest rate is divided by 360 and the loan term is multiplied by 360. Using the same example as above, the formula would be: =PMT(0.05/360, 5*360, -10000). This will yield a slightly different monthly payment amount compared to the 365-day method.
Building a Loan Amortization Schedule
To create a comprehensive amortization schedule, you’ll need to set up columns for: Period, Beginning Balance, Payment, Interest, Principal, and Ending Balance.
The first row contains the initial loan amount in the “Beginning Balance” column. The payment is calculated using the PMT formula (either 365 or 360-day method). The interest for the first period is calculated by multiplying the beginning balance by the daily interest rate (annual rate / 365 or 360) and the number of days in the period (usually 30 for monthly payments). The principal paid is the payment minus the interest. The ending balance is the beginning balance minus the principal paid. Subsequent rows repeat this process, using the ending balance from the previous row as the beginning balance for the next. The formulas are copied down to cover the entire loan term.
Incorporating Different Interest Rates and Loan Terms
The flexibility of Excel allows for easy adjustment of interest rates and loan terms. Simply change the values in the cells representing the annual interest rate (rate) and the loan term in years (nper) in your PMT formula and the amortization schedule will automatically recalculate. You can create input cells for these values, allowing users to easily modify parameters and see the impact on the loan payments and amortization schedule. For instance, you could create a cell labeled “Annual Interest Rate” and another labeled “Loan Term (Years)”, then reference those cells in your formulas. This enables “what-if” scenarios, allowing users to explore different loan options.
Visualizing Loan Data with Excel Charts
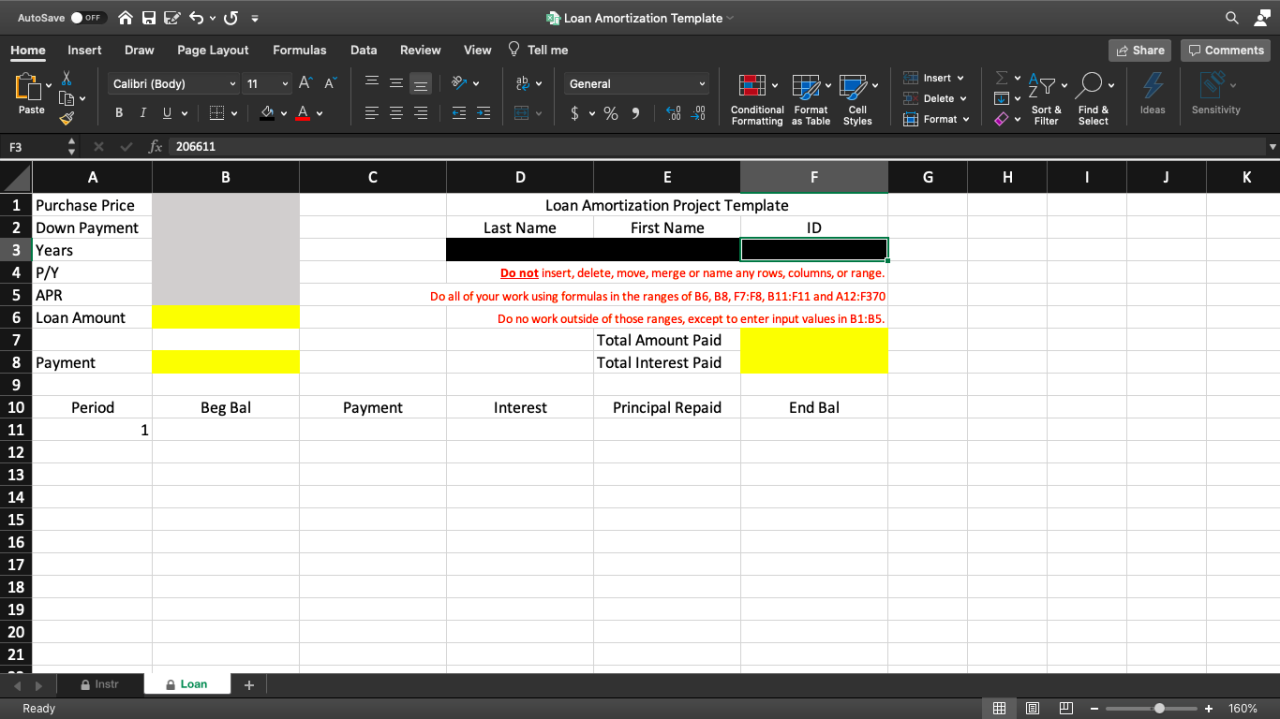
Data visualization is crucial for understanding the nuances of 365/360 loan calculations. By transforming raw numerical data into compelling charts, you can quickly grasp the impact of different calculation methods on key loan metrics like total interest paid and monthly payments. This allows for more informed financial decisions.
Excel offers a powerful suite of charting tools perfectly suited for this task. Let’s explore how to effectively visualize the differences between 365-day and 360-day loan calculations.
Comparison of Total Interest Paid
A column chart is the most effective way to visually compare the total interest paid over the loan’s lifetime using the 365-day and 360-day methods. The simplicity of a column chart allows for immediate comprehension of the difference. To create this chart, first calculate the total interest paid for each method in separate cells. Then, select both data points and choose the “Column Chart” option from Excel’s chart menu.
The chart should clearly label each column with the day count method (e.g., “365-Day Method,” “360-Day Method”) and include a descriptive title such as “Total Interest Paid Comparison: 365 vs. 360-Day Methods.” Consider adding data labels directly to the columns to display the exact interest amounts for better clarity. Adjusting the chart’s colors and font sizes will further improve readability. For example, you might use contrasting colors to highlight the difference and a larger font size for the title and labels. Imagine a vibrant chart with a clear blue column representing the 365-day method and a contrasting orange column for the 360-day method, immediately showing which method results in higher interest payments. The difference in the column heights will visually represent the magnitude of the interest difference.
Monthly Payment Breakdown
To illustrate the monthly payment differences, a line chart provides an excellent visualization. For each month of the loan term, calculate the payment amount using both the 365-day and 360-day methods. Enter this data into Excel, with one column representing the month number, and two columns for the payment amounts under each method.
Select the data and create a line chart. Each line will represent a calculation method. Use distinct colors and clearly label each line with the corresponding method (e.g., “365-Day Method,” “360-Day Method”). The x-axis should represent the month number, and the y-axis should represent the payment amount. A descriptive title such as “Monthly Payment Comparison: 365 vs. 360-Day Methods” is crucial. Adding a legend further enhances readability. For improved visual appeal, consider using a professional color scheme and adjusting the line thickness for better distinction. This chart will vividly demonstrate the slight variations in monthly payments across the loan term resulting from the different day-count conventions. For instance, a longer loan might show a more significant divergence between the two lines over time.
Advanced Features of a 365/360 Loan Calculator in Excel
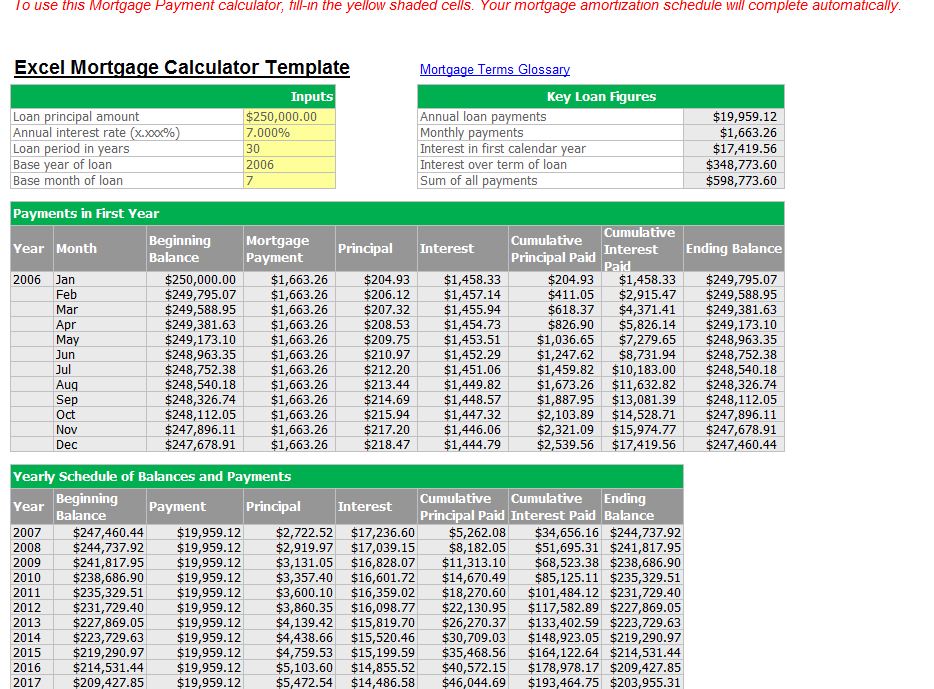
Building a basic 365/360 loan calculator in Excel is straightforward. However, to create a truly powerful and reliable tool, you need to incorporate advanced features that handle real-world complexities and prevent user errors. This goes beyond simple calculations and delves into robust error handling and user-friendly design. Let’s explore these critical enhancements.
Significant Impacts of Choosing 365 vs. 360-Day Methods, 365 360 loan calculator excel
The choice between the 365-day and 360-day methods can significantly affect the borrower’s total interest paid, especially for longer loan terms. The 360-day method, while simplifying calculations, results in slightly higher interest charges. Consider a $100,000 loan at 5% interest over 30 years. Using a 365-day method might result in a total interest paid of $90,000, while the 360-day method could lead to approximately $92,000. This seemingly small difference compounds over time, representing a substantial amount for the borrower. The difference is most pronounced in longer-term loans. Therefore, transparency and understanding of the chosen method are crucial for the borrower.
Implications of Different Compounding Frequencies
The frequency of compounding (daily, monthly, quarterly, annually) directly impacts the total interest accrued. Daily compounding, while more precise, leads to slightly higher interest payments compared to monthly or annual compounding. Our Excel calculator should allow users to select the compounding frequency. For example, a $50,000 loan at 6% annual interest compounded daily versus annually will result in a higher total interest paid with daily compounding due to the more frequent calculation of interest on interest. This difference, although seemingly small on a single compounding period, becomes more significant over the loan term. The calculator should clearly display the effect of the chosen compounding frequency on the total interest and the monthly payment.
Incorporating Additional Fees into Loan Calculations
Real-world loans often involve additional fees such as origination fees, processing fees, or prepayment penalties. These fees should be integrated into the Excel calculator to provide a more accurate representation of the loan’s total cost. The calculator should allow users to input these fees, and the calculation should incorporate them into the total loan amount and monthly payment. For example, a $200,000 loan with a 2% origination fee ($4,000) will increase the total loan amount to $204,000, affecting the monthly payment accordingly.
Utilizing Data Validation for Accurate Inputs
Data validation is crucial to prevent incorrect inputs and ensure the accuracy of the loan calculations. The Excel calculator should utilize data validation to restrict input values to appropriate ranges and data types. For instance, interest rates should be limited to a reasonable range (e.g., 0% to 20%), loan amounts should be positive numbers, and loan terms should be positive integers. Error messages should be displayed if invalid data is entered. This proactive approach prevents erroneous calculations and ensures the reliability of the calculator’s output.
Error Handling Techniques for Robustness
Several error handling techniques can significantly improve the calculator’s robustness. First, the calculator should include checks for division by zero errors, which could occur if the loan term is zero. Second, it should handle non-numeric inputs gracefully, preventing crashes and displaying informative error messages. Third, the use of IFERROR functions can handle potential errors in individual calculations, preventing the entire calculator from failing due to a single error. These features enhance the user experience and prevent unexpected results. Robust error handling makes the calculator more user-friendly and reliable.
Illustrative Examples of Loan Calculations: 365 360 Loan Calculator Excel
Understanding the nuances of 365-day versus 360-day loan calculations is crucial for accurate financial modeling. The choice between these methods significantly impacts the total interest paid over the loan’s lifetime, and the difference can be substantial, especially for larger loans or longer terms. Let’s explore scenarios where each method yields a lower total interest cost.
Scenario: 360-Day Method Results in Lower Total Interest Cost
Consider a $100,000 loan with a 5% annual interest rate, amortized over 1 year. Using the 360-day method, the daily interest rate is approximately 0.05/360 = 0.0001389. The total interest accrued over the year will be calculated based on this daily rate multiplied by the outstanding principal balance for each day. In contrast, the 365-day method would use a daily rate of approximately 0.05/365 = 0.000137. While seemingly insignificant, this small difference in daily interest rates, compounded over the 360 or 365 days, will result in a slightly lower total interest cost with the 360-day method. The exact difference will depend on the amortization schedule and the method used to calculate interest (simple vs. compound). In this specific example, the difference might be small, but for longer loan terms, the cumulative effect becomes more pronounced. The 360-day method’s slightly higher daily interest rate is offset by the fewer days used in the calculation.
Scenario: 365-Day Method Results in Lower Total Interest Cost
This scenario requires a longer loan term and a higher interest rate to highlight the differences more significantly. Let’s examine a $500,000 loan with an 8% annual interest rate over a 5-year term. The cumulative effect of the higher number of days (365) in the 365-day method’s calculation will lead to slightly more frequent compounding and ultimately, a slightly higher total interest paid compared to the 360-day method. However, the smaller daily interest rate used in the 365-day method can, in certain situations, particularly with longer terms and higher interest rates, result in a lower total interest paid. The key here is the interplay between the daily interest rate and the number of days used in the calculation, with the impact of the longer term magnifying the difference.
Factors Influencing the Choice Between Calculation Methods
Several factors influence the selection of the 365-day or 360-day method in real-world applications. These include:
- Industry Conventions: Certain industries may favor one method over the other due to established practices or regulatory requirements. For example, the mortgage industry frequently uses the 360-day method.
- Loan Type: The type of loan significantly influences the chosen calculation method. Some loan types might stipulate a specific method in their terms and conditions.
- Legal and Regulatory Compliance: Laws and regulations may dictate the acceptable calculation methods within specific jurisdictions.
- Risk Assessment: Lenders might consider the risk associated with a particular loan and select a method that aligns with their risk appetite.
Impact of Loan Term Length on the Difference Between Calculation Methods
The difference between the 365-day and 360-day methods becomes more pronounced as the loan term lengthens. In short-term loans, the difference in total interest paid is often negligible. However, with longer-term loans (e.g., mortgages), the cumulative effect of the slightly different daily interest rates leads to a more significant disparity in the total interest paid. This is because the compounding effect has more time to accumulate differences. The longer the loan, the greater the potential for a substantial difference in total interest cost.
Analyzing Loan Scenarios with the Excel Calculator
The Excel calculator simplifies the analysis of various loan scenarios. By inputting different interest rates and loan terms, users can quickly observe the impact on total interest cost under both the 365-day and 360-day methods. For example, by varying the interest rate from 4% to 10% and the loan term from 1 to 30 years, one can generate a table illustrating the difference in total interest cost under each method. This allows for a comprehensive comparison and informed decision-making. The calculator facilitates “what-if” scenarios, enabling users to explore the sensitivity of the total interest cost to changes in interest rates and loan terms. This empowers borrowers and lenders to make well-informed decisions.